GRAFOS EN C

Los grafos no son más que la versión general de un árbol, es decir, cualquier nodo de un grafo puede apuntar a cualquier otro nodo de éste (incluso a él mismo). Este tipo de estructuras de datos tienen una característica que lo diferencia de las estructuras que hemos visto hasta ahora: los grafos se usan para almacenar datos que están relacionados de alguna manera (relaciones de parentesco, puestos de trabajo, ...); por esta razón se puede decir que los grafos representan la estructura real de un problema. En lo que a ingeniería de telecomunicaciones se refiere, los grafos son una importante herramienta de trabajo, pues se utilizan tanto para diseño de circuitos como para calcular la mejor ruta de comunicación en Internet.

Terminología de grafos: 

 Vértice : Nodo.

Enlace : Conexión entre dos vértices (nodos).

Adyacencia : Se dice que dos vértices son adyacentes si entre ellos hay un enlace directo.

Vecindad : Conjunto de vértices adyacentes a otro.

 Camino : Conjunto de vértices que hay que recorrer para llegar desde un nodo origen hasta un nodo destino.

Grafo conectado : Aquél que tiene camino directo entre todos los nodos.

 Grafo dirigido : Aquél cuyos enlaces son unidireccionales e indican hacia donde están dirigidos.

Gafo con pesos : Aquél cuyos enlaces tienen asociado un valor. En general en este tipo de grafos no suele tener sentido que un nodo se apunte a sí mismo porque el coste de este enlace sería nulo.

Representación en memoria de un grafo: 

Una característica especial en los grafos es que podemos representarlos utilizando dos estructuras de datos distintas. En los algoritmos que se aplican sobre ellos veremos que adoptarán tiempos distintos dependiendo de la forma de representación elegida. En particular, los tiempos de ejecución variarán en función del número de vértices y el de aristas, por lo que la utilización de una representación u otra dependerá en gran medida de si el grafo es denso o disperso.

Para nombrar los nodos utilizaremos letras mayúsculas, aunque en el código deberemos hacer corresponder cada nodo con un entero entre 1 y V (número de vértices) de cara a la manipulación de los mismos.

Representación por matriz de adyacencia

Es la forma más común de representación y la más directa. Consiste en una tabla de tamaño V x V, en que la que a[i][j] tendrá como valor 1 si existe una arista del nodo i al nodo j. En caso contrario, el valor será 0. Cuando se trata de grafos ponderados en lugar de 1 el valor que tomará será el peso de la arista. Si el grafo es no dirigido hay que asegurarse de que se marca con un 1 (o con el peso) tanto la entrada a[i][j] como la entrada a[j][i], puesto que se puede recorrer en ambos sentidos.

int V,A;

int a[maxV][maxV];

{
void inicializar()

  char v1,v2;
int i,x,y,p;
  // Leer V y A

  for (i=1; i<=A; i++)
memset(a,0,sizeof(a));
  { 

    x=v1-'A'; y=v2-'A';
scanf("%c %c %d\n",&v1,&v2,&p);
    a[x][y]=p; a[y][x]=p;

}

  } 

Representación por lista de adyacencia

Otra forma de representar un grafo es por medio de listas que definen las aristas que conectan los nodos. Lo que se hace es definir una lista enlazada para cada nodo, que contendrá los nodos a los cuales es posible acceder. Es decir, un nodo A tendrá una lista enlazada asociada en la que aparecerá un elemento con una referencia al nodo B si A y B tienen una arista que los une. Obviamente, si el grafo es no dirigido, en la lista enlazada de B aparecerá la correspondiente referencia al nodo A.

Las listas de adyacencia serán estructuras que contendrán un valor entero (el número que identifica al nodo destino), así como otro entero que indica el coste en el caso de que el grafo sea ponderado. En el ejemplo se ha utilizado un nodo z ficticio en la cola (ver listas, apartado cabeceras y centinelas).

struct nodo
{
  int v;

  nodo *sig;
int p;
};


int V,A;  // vértices y aristas del grafo
struct nodo *a[maxV], *z;

void inicializar()
{

  z=(struct nodo *)malloc(sizeof(struct nodo));
int i,x,y,peso;
  char v1,v2;
  struct nodo *t;
  z->sig=z;

    scanf("%c %c %d\n",&v1,&v2,&peso);
for (i=0; i<V; i++)
    a[i]=z;
  for (i=0; i<A; i++)
  {
    x=v1-'A'; y=v2-'A';

    t->v=y; t->p=peso; t->sig=a[x]; a[x]=t;
t=(struct nodo *)malloc(sizeof(struct nodo));


    t->v=x; t->p=peso; t->sig=a[y]; a[y]=t;
t=(struct nodo *)malloc(sizeof(struct nodo));
  }

}

En este caso el espacio ocupado es O(V + A), muy distinto del necesario en la matriz de adyacencia, que era de O(V²). La representación por listas de adyacencia, por tanto, será más adecuada para grafos dispersos.

Exploración de grafos

A la hora de explorar un grafo, nos encontramos con dos métodos distintos. Ambos conducen al mismo destino (la exploración de todos los vértices o hasta que se encuentra uno determinado), si bien el orden en que éstos son "visitados" decide radicalmente el tiempo de ejecución de un algoritmo, como se verá posteriormente.

En primer lugar, una forma sencilla de recorrer los vértices es mediante una función recursiva, lo que se denomina búsqueda en profundidad. La sustitución de la recursión (cuya base es la estructura de datos pila) por una cola nos proporciona el segundo método de búsqueda o recorrido, la búsqueda en amplitud o anchura.

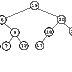
Suponiendo que el orden en que están almacenados los nodos en la estructura de datos correspondiente es A-B-C-D-E-F... (el orden alfabético), tenemos que el orden que seguiría el recorrido en profundidad sería el siguiente:

A-B-E-I-F-C-G-J-K-H-D

En un recorrido en anchura el orden sería, por contra:

A-B-C-D-E-G-H-I-J-K-F

Es decir, en el primer caso se exploran primero los verdes y luego los marrones, pasando primero por los de mayor intensidad de color. En el segundo caso se exploran primero los verdes, después los rojos, los naranjas y, por último, el rosa.

Es destacable que el nodo D es el último en explorarse en la búsqueda en profundidad pese a ser adyacente al nodo de origen (el A). Esto es debido a que primero se explora la rama del nodo C, que también conduce al nodo D.

En estos ejemplos hay que tener en cuenta que es fundamental el orden en que los nodos están almacenados en las estructuras de datos. Si, por ejemplo, el nodo D estuviera antes que el C, en la búsqueda en profundidad se tomaría primero la rama del D (con lo que el último en visitarse sería el C), y en la búsqueda en anchura se exploraría antes el H que el G.