Un árbol AVL es un árbol binario de búsqueda (ABB) que tiene como característica que siempre esta balanceado; que se le añade una condición de equilibrio. esta condición es que para todo nodo ,la altura de sus subárboles...
Los grafos no son más que la versión general de un árbol, es decir, cualquier nodo de un grafo puede apuntar a cualquier otro nodo de éste (incluso a él mismo). Este tipo de estructuras de datos tienen...
Un árbol binario es una estructura de datos en la cual cada nodo puede tener un hijo izquierdo y un hijo derecho. No pueden tener más de dos hijos (de ahí el nombre "binario"). Si algún hijo tiene como referencia a null, es decir...
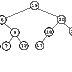
Los árboles-B+ se han convertido en la técnica mas utilizada para la organización de archivos indizados. La principal característica de estos arboles es que todas las claves se encuentran en las hojas y por lo tanto cualquier camino...
